Nomenclatura básica de redes neuronales

Uno de los problemas más frecuentes cuando escribimos un artículo o leemos sobre temas complejos como redes neuronales, es sin duda alguna entender la nomenclatura asociada a cada fórmula, es por eso que en este apartado hablaremos sobre como entender de una manera práctica y sencilla las nomenclaturas usadas en AI.

Vamos a suponer que queremos realizar un clasificador binario que nos diga si existe o no un perro en la siguiente foto

esto es:

1 –> (perro)

0 –> (no perro)

donde 0 y 1 representan la salida de nuestro clasificador , matemáticamente representado por la letra ‘y’ también conocida como etiqueta o label

Sin embargo, presentar una imagen a un computador y que la interprete no es una tarea simple, ya que las imágenes tradicionales que conocemos son la representación de una matriz de números con diferentes valores (conocidos como pixeles), los cuales representan la intensidad del color. Sin embargo no solo se trata de una matriz que representa todos los posibles colores, cada color viene representado por su propia matriz, asi al final una foto tradicional en el formato RGB no es más que una superposición de capas con diferentes colores, como se puede ver en la siguiente imagen.

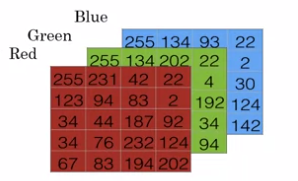
Ahora, asumiendo que nuestra imagen es de un tamaño de 64x64 pixeles, lo que quiere decir que cada canal de color tambíen tiene la misma dimension, es hora de presentarle esa informacion a nuestro ordenador, pero para eso estas intensidades de color (pixeles) se deben presentar como un vector de caracteristicas donde cada fila de nuestras matrices RGB sera puesta en una sola columna, una detras de otra para formar asi un vector de características de 1xN, donde N sera la dimensión de nuestra imágen en nuesro ejemplo (64x64).

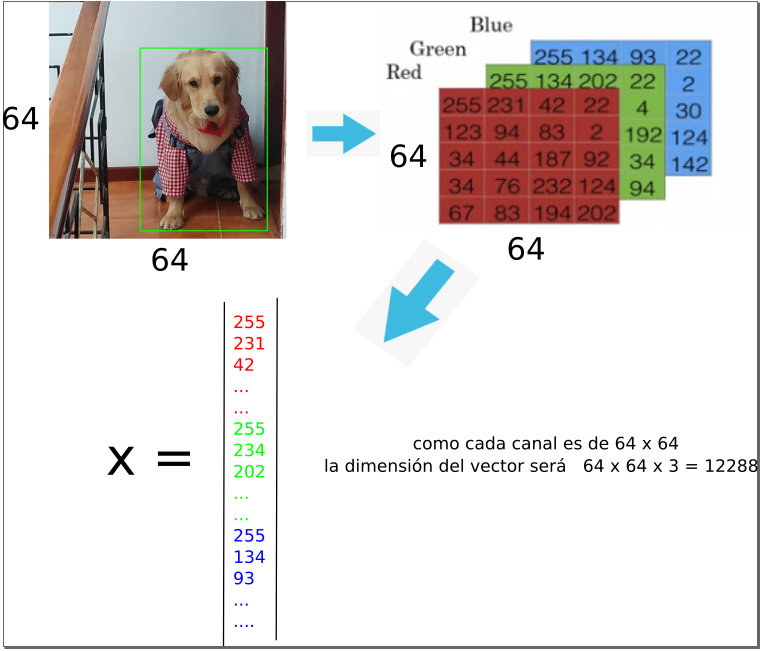
de esta forma nuestro vector (x) de características de entrada RGB será representado por: \(N_{x}= 12288\)

Retornando a nuestro ejemplo de clasificación lo podemos resumir de las siguiente manera,:

x –> representa las entradas de la imagen

y –> corresponde a su respectiva predicción con valores 1 ó 0, indicándonos si la imagen contiene un perro o no.

Teniendo en cuenta lo anterior, nuestro conjunto de datos de entrenamiento quedaría representado por pares de valores:

\[(x,y) \; donde \; x \in \; \Re^{N_{x}} \; and \; y \; \in \; (0,1)\]

Por otro lado como sabemos, nuestro conjunto de datos de entrenamiento está compuesto por un número M de ejemplos que se representan de la siguiente manera:

\[M_{train} = (x^{(1)}, y^{(1)}),\; (x^{(2)}, y^{(2)}), \; (x^{(m)}, y^{(m)})\]

y de la misma forma tendremos nuestro conjunto de test:

\[M_{test} = (x^{(1)}, y^{(1)}),\; (x^{(2)}, y^{(2)}), \; (x^{(m)}, y^{(m)})\]

Finalmente para poner todos nuestros conjuntos de datos tanto de entrenamiento como de test, en una notación compacta, definimos la forma matricial del vector x:

\[\begin{equation} X = \begin{bmatrix} ... & ... & ...\\ x^{(1)} & x^{(2)} & x^{(m)}\\ ... & ... & ... \end{bmatrix} \end{equation}\]

donde m es el número de datos (ejemplos) de entrenamiento puestos en columnas, y las filas es la cantidad de datos de información de cada ejemplo como en nuestro ejemplo \(N_{x}=12288\) quedando nuestra dimensión final con la siguiente nomenclatura:

\[X \in \; \Re^{N_{x} \; \times \; m}\]

que viéndolo desde código python sería

\[X.shape =(N_{x},m)\]

Finalmente las salidas o labels ‘y’, puede representarse matricialmente de la siguiente manera

\[\begin{equation} Y = \begin{bmatrix} y^{(1)} & y^{(2)} & y^{(m)} \end{bmatrix} \end{equation}\]

con la siguiente nomenclatura

\[y \in \; \Re^{1 \; \times \; m}\]

que viéndolo desde código python sería

\[y.shape =(1,m)\]